On May 24, 2000, the Clay Mathematics Institute announced to the world the seven Millennium Prize problems, which are known as the "Seven Mathematical Problems to Solve in the 21st Century".
These include the proven Poincaré conjecture and the famous Riemann Conjecture. Anyone who solves one of these problems will receive a prize of $1 million.
However, among these seven problems, there is one problem that is extraordinary, and if that problem is proved, then the rest of the problems will be solved. This is the P/NP problem.
In the movie "Charlie and the Chocolate Factory", "Willy Wonka" chocolate is extremely popular among children, but the production of these chocolates is a very mysterious factory, which also aroused widespread curiosity in the world.

The owner of the chocolate factory, Willy Wonka, put five golden tickets in the hundreds of chocolates he sold, and those who found the tickets could get a chance to visit the chocolate factory.

The question arises, how to buy chocolate with golden coupons in the most efficient way? The answer is as simple as buying the chocolate with the golden ticket the first time or asking your hundreds of employees to keep unwrapping the chocolate wrappers day and night, just like the father in the movie.
But eventually, no matter what method is used, five people will definitely find these five golden tickets.
This is an example of a P/NP problem, where NP is the set of all solutions that exist for this event, and P is the set of solutions that can find this answer quickly. The specific content of the P/NP problem is to explore how to find the fastest answer.
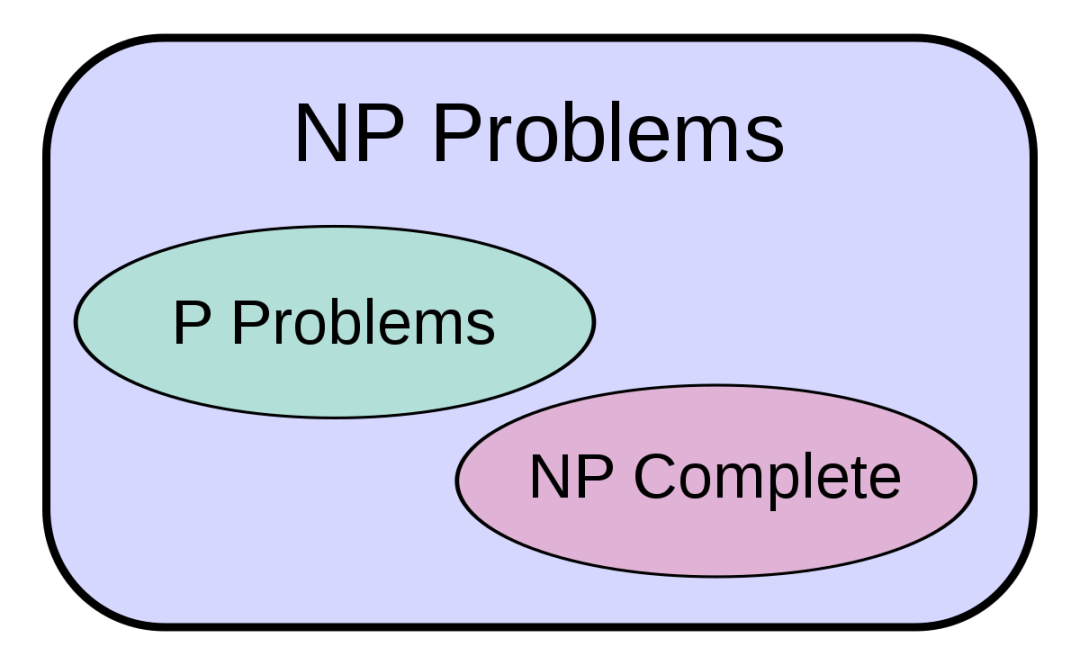
Somewhat abstract, then give another example:
There is an eight-digit number, 12186984, and I used two numbers multiplied together to get this number, and I would like you to find the two factors I used and tell me about them. I will let you know if the answer matches mine.
In this problem, there is one and only one correct answer, and that is 1234*9876. If you use short division and a certain amount of time, you will definitely come up with this answer, but what if you get a ten-digit number or a fifty-digit number?
At this point, you would consider using a computer program to project all the possibilities, all these factors, which are the NP part of the P/NP problem, and the P part is the fastest way for you to get the correct answer, which is the only correct answer.
More simply put, if you solve the P/NP problem, you can quickly know the answers to all the questions that require making choices. This is why I say that the rest of the millennial math puzzle will be solved as well because based on the answers to the P/NP problems, you can know exactly whether you are going in the right direction with your deduction.
This also answers the question in the title of this article, how to become an omniscient person? If you have solved the P/NP problem, you are close to knowing the answer to all the questions.
So how exactly can the P/NP problems be used in our life?
The core of the most widely used RSA encryption method is based on the principle that NP ≠ P. The general content is the same as the example I gave in the previous article, that is, knowing the product of two factors can be known, but knowing only a large number but not knowing the specific two solutions.
So once P=NP, all these current encryption programs will fail. The first to be affected must be the most widely used social networking APP because this social networking software through RSA encryption to confirm that an account can only correspond to one user. Once RSA encryption fails, the passwords of these accounts will be obvious to those who know some technology.
There are certainly good aspects - again, in the social networking APP space.
The way to increase the profitability of social software is to increase the number of users. So what is the purpose of users using social software, naturally, is to socialize. This may sound like nonsense, but socializing includes not only socializing with acquaintances but also socializing between strangers, including business dealings and cultural exchanges.
So how can we help users find people they can relate to and create value? Here it is necessary to mention Six Degrees of Separation or the Theory of Six People.
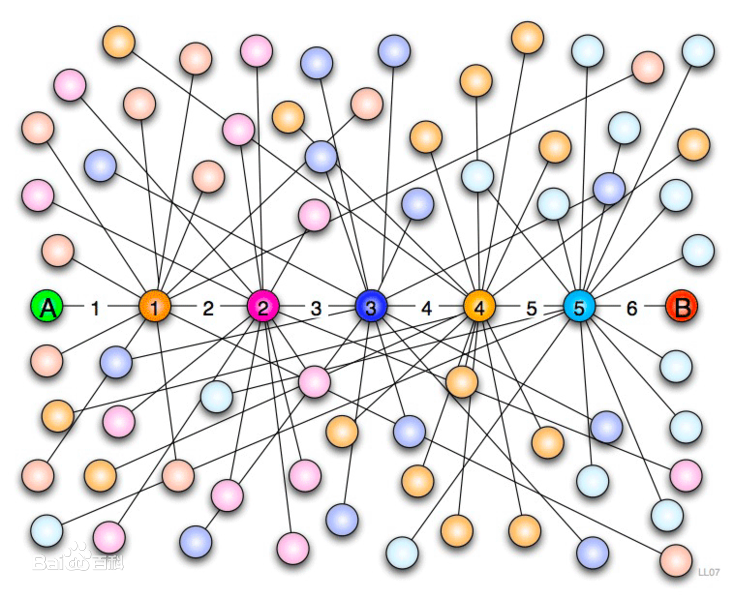
The core of this theory is that any two strangers who do not know each other can get to know each other through an average of five people who know each other in sequence.
For example, I have never met Russian President Vladimir Putin, but if I had wanted to, I could have been introduced to Putin by five people.
Under the existing circumstances, I conservatively estimate that it will be difficult for me to get acquainted with Putin before I turn eighty because I don't know exactly who is the fastest way to get acquainted with Putin.
But what if P=NP? Social software can quickly find the people users want to meet through their interests, thus creating more efficient social interaction.
It can also be used in medicine - for example, in the treatment of cancer. The essence of cancer is that mutations in some cells cause intense proliferation, so if you find a way to stop these cells from continuing to proliferate, you can treat cancer.
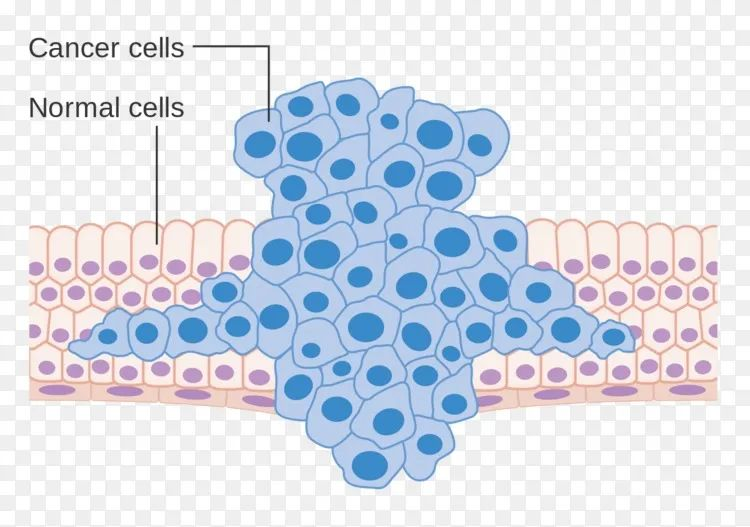
By solving the P=NP problem, the computer was able to calculate the normal and mutated DNA of each person in a very short time, and then create a protein with a specific folding pattern to "gag" the cancer cells, which would then starve to death, and cancer would be cured.
What is even more desirable is that the cost of this treatment includes only the cost of electricity, which the computer rarely uses to calculate, and the cost of folding the protein. And currently, specific shapes of proteins can even be achieved by 3D printing.
There are quite a few more - in machine learning, for example. Today's big data technology is developing rapidly, and artificial intelligence development is being promoted rapidly through continuous machine learning. But there are still drawbacks, and the base content of machine learning is very huge.
For example, to recognize handwriting, it is not enough for the machine to learn to recognize two or three ways of writing the number 5, but at least thousands of pictures containing different ways of writing 5.
But what if P=NP? The programmer can work out exactly which photos to use to achieve a very high level of accuracy in machine recognition. The savings in resources and time would be unimaginable.

You may be very surprised to see that a small mathematical problem can evolve into an algorithm. And it is surprising that this algorithm has such infinite power to accomplish so many challenges. It does sound unlikely because most of the current human perception is based on P ≠ NP. But since this is a mathematical problem, it has the possibility of being proved. Wasn't Fermat's Grand Theorem, which previously defeated mathematicians from all over the world, also defeated at the feet of human civilization.
So what I have stated in the previous article is not a fantasy, but a possible future.




Comments